Pulse Amplitude Modulation (PAM)
Pulse Amplitude Modulatin (PAM)
Pulse amplitude modulation is a type of modulation in which the amplitudes of regularly spaced rectangular pulses vary according to instantaneous value of the modulating or message signal.
In fact, the pulses in a PAM signal may be of flat top type or natural type or ideal type.
Out of all the three pulse amplitude modulation methods, the flat top PAM is most popular and is widely used.
The reason for using flat top PAM is that during the transmission, the noise interferes with the top of the transmitted pulses and this noise can be easily removed if the PAM pulse has flat top.
However, in case of natural samples PAM signal, the pulse has varying top in accordance with the signal variation.
Now, when such type of pulse is received at the receiver, it is always contaminated by noise.
Then it becomes quite difficult to determine the shape of the top of the pulse and thus amplitude detection of the pulse is not exact.Due to this, errors are introduced in the received signal.
Therefore, flat top sampled PAM is widely used.
Fig.1 shows the sample and hold circuit to produce flat top sampled PAM and the waveform for flat top sampled PAM.
Fig.1 : (a) Sample and hold circuit generating flat top sampled PAM, (b) Waveforms of flat top sampled PAM
Principle of Working
A sample and hold circuit shown in fig.1 is used to produce Flat top sampled PAM. The working principle of this circuit is quite easy.
The sample and Hold (S/H) circuit consists of two field effect transistors (FET) switches and a capacitor.
The sampling switch is closed for a short duration by a short pulse applied to the gate G1 of the transistor.
During this period, the capacitor ‘C’ is quickly charged upto a voltage equal to the instantaneous sample value of the incoming signal x(t).
Now, the sampling switch is opened and the capacitor ‘C’ holds the charge.
The discharge switch is then closed by a pulse applied to gate G2 of the other transistor.
Due to this, the capacitor ‘C’ is discharged to zero volts. The discharges switch is then opened and thus capacitor has no voltage.
Hence, the output of the sample and hold circuit consists of a sequence of flat top samples as shown in fig.1(b).
Mathematical Analysis
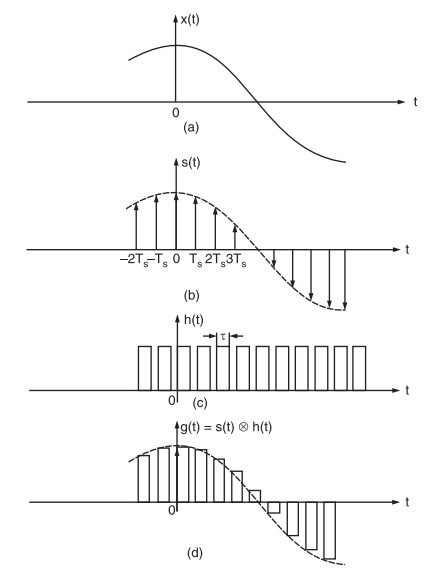
In a flat top PAM, the top of the samples remains constant and is equal to the instantaneous value of the baseband signal x(t) at the start of sampling.
The duration or width of each sample is τ and sampling rate is equal to,
From fig.1 (b), it may be noted that only starting edge of the pulse represents instantaneous value of the baseband signal x(t).
Also, the flat top pulse of g(t) is mathematically equivalent to the convolution of instantaneous sample and a pulse h(t) as depicted in fig.2.
Fig.2 : Convolution of any function with delta function is equal to that function
This means that the width of the pulse in g(t) is determined by the width of h(t) and the sampling instant is determined by the delta function.
In fig.1 (b), the starting edge of the pulse represents the point where baseband signal is sampled and width is determined by function h(t).
Therefore, g(t) will be expressed as,
………… (1)
This equation has been explained in fig.3 below.
Fig.3 : (a) Baseband signal x(t), (b) Instantaneously sample signal s(t), (c) Constant pulse width function h(t), (d) Flat top sampled PAM signal g(t) obtained through convolution of h(t) and s(t).
Now, from the property of delta function, we know that for any function f(t),
…………… (2)
This property is used to obtain flat top samples. It may be noted that to obtain flat top sampling, we are not applying the equation (2) directly here i.e., we are applying a modified form of equation (2). This modified equation is equation (1).
Thus, in this modified equation, we are taking s(t) in place of delta functions δ(t). Observe that δ(t) is a constant amplitude delta function whereas s(t) is a varying amplitude train of impulses. This means that we are taking s(t) which is an instantaneously sampled signal and this is convolved with function h(t) as in equation (1). Therefore, on convolution of s(t) and h(t), we get a pulse whose duration is equal to h(t) only but amplitude is defined by s(t).
Now, we know that the train of impulses may be represented mathematically as,
The signal s(t) is obtained by multiplication of baseband signal x(t) and δTs (t). Thus,
Or,
Now, sampled signal g(t) is given as equation (1)
According to shifting property of delta function, we know that,
Hence,
This equation represents value of g(t) in terms of sampled value x(nTs) and function h(t – nTs) for flat top sampled signal. Now, again from equation (1), we have
Taking Fourier transform of both sides of above equation, we get
We know that S(f) is given as
Therefore,
Thus, spectrum of flat top PAM signal:
Here, H(f) is the Fourier transform of the rectangular pulse. The spectrum of this rectangular pulse is shown in fig.4(b).
Let the spectrum of s(t) be the rectangular pulse train as shown in fig.4(a) and the spectrum of h(t) i.e., H(f) is shown in fig.4(b).
Fig.4 : (a) Spectrum of some arbitrary signal. The signal is sampled at fs and maximum frequency in the signal is fm, (b) Spectrum of flat top signal. The dotted curve is H(f) = τ sin c(fτ)
we know that,
Thus, according to above equation, we can plot the spectrum G(f) as shown in fig.4(b).
It may be observed in fig.4(b) that higher frequencies in S(f) are attenuated due to roll-off characteristics of the ‘sinc’ pulse. This effect is popularly known as aperture effect. An equalizer is needed to overcome this effect.