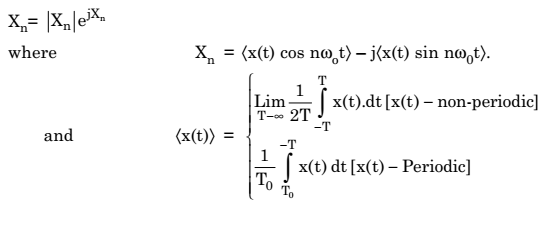Short Questions and Answers on Signal Analysis and Transmission
Q.1. What is Fourier series as a complex Exponential?
Ans.
Q.2. What are Fourier coefficients in time averages?
Ans.
Q.3. What is Fourier Integral?
Ans.
Q.4. State the superposition theorem of Fourier transform.
Ans.
Q.5. State the Time-delay theorem of Fourier transform.
Ans.
Q.6. Write down the scale-change theorem of Fourier-Transform.
Ans.
Q.7. Write down the duality Theorem of Fourier Transform.
Ans.
Q.8. Write the Frequency Translation Theorem of Fourier Transform.
Ans.
Q.9. Write the modulation Theorem of Fourier Transform.
Ans.
Q.10. State the differentiation Theorem of Fourier Transform.
Ans.
Q.11. State the Integration Theorem of Fourier Transform.
Ans.
Q.12. State the convolution Theorem of Fourier Transform.
Ans.
Q.13. State the multiplication Theorem of Fourier Transform.
Ans.
Q.14. What is dirac-delta function?
Ans.
Q.15. State the properties of dirac-delta function.
Ans.
Q.16. State and prove the two convolution theorems.
Ans. The two convolution theorems are:
Q.17. An audio oscillator is switched on at t = 0. Find the spectrum of the generated. (i) Cosine waveform (ii) Sine waveform both of frequency ω0.
Ans.
The sine and cosine waveforms will be present only after t = 0. That means:
Q.18. What is the difference between time domain representation and frequency domain representation of signals?
Ans. In the time domain representation of a signal, we plot the variation in signal amplitude, with respect to time. It gives us an idea about the shape of the signal in time domain.
In the frequency domain representation we plot the amplitude and phase of various frequency components with respect to frequency. It tells us about what all frequency components are present inside a given time domain signal and the proportion in which they are mixed together.